‘Independence’ is another key term in statistics. We will see several different kinds of independence, but in general it is about whether one measurement, or factor gives information about another.
‘Independence’ is another key term in statistics. We will see several different kinds of independence, but in general it is about whether one measurement, or factor gives information about another.
Non-independence may increase variability, lead to misattribution of effects or even suggest completely the wrong effect.
Simpson’s paradox is an example of the latter where, for example, you might see on year on year improvement in the performance of each kind of student you teach and yet the university tells you that you are doing worse!
Imagine you have tossed a coin ten times and it has come up heads each time. You know it is a fair coin, not a trick one. What is the probability it will be a tail next?
Of course, the answer is 50:50, but we often have a gut feeling that it should be more likely to be a tail to even things out. This is the uniformity fallacy that leads people to choose the pattern with uniformly dispersed drops in the Gheisra story. It is exactly the same feeling that a gambler has putting in a big bet after a losing streak, “surely my luck must change”.
In fact with the coin tosses, each is independent: there is no relationship between one coin toss and the next. However, there can be circumstances (for example looking out of the window to see it is raining), where successive measurements are not independent.
This is the first of three kinds of independence we will look at :
- measurements
- factor effects
- sample prevalence
These each have slightly different causes and effects. In general the main effect of non-independence is to increase variability, however sometimes it can also induce bias. Critically, if one is unaware of the issues it is easy to make false inferences: I have looked out of the window 100 times and it was raining each time, should I therefore conclude that it is always raining?
We have already seen an example of where successive measurements are independent (coin tosses) and when they are not (looking out at the weather). In the latter case, if it is raining now it is likely to be if I look again in two minutes, the second observation adds little information.
Many statistical tests assume that measurements are independent and need some sort of correction to be applied or care in interpreting results when this is not the case. However there are a number of ways in which measurements may be related to one another:
order effects – This is one of the most common in experiments with users. A ‘measurement’ in user testing involves the user doing something, perhaps using a particular interface for 10 minutes. You then ask the same user to try a different interface and compare the two. There are advantages of having the same user perform on different systems (reduces the effect of individual differences); however, there are also potential problems.
You may get positive learning effects – the user is better at the second interface because they have already got used to the general ideas of the application in the first. Alternatively there may be interference effects, the user does less well in the second interface because they have got used to the detailed way things were done in the first.
One way this can be partially ameliorated is to alternate the orders, for half the users they see system A first followed by system B, the other half sees them the other way round. You may even do lots of swops in the hope that the later ones have less order effects: ABABABABAB for some users and BABABABABA for others.
These techniques work best if any order effects are symmetric, if, for example, there is a positive learning effects between A and B, but a negative interference effect between B and A, alternating the order does not help! Typically you cannot tell this from the raw data, although comments made during talk-aloud or post study interviews can help. In the end you often have to make a professional judgment based on experience as to whether you believe this kind of asymmetry is likely, or indeed if order effects happen at all
context or ‘day’ effects – Successively looking out of the window does not give a good estimate of the overall weather in the area because they are effectively about the particular weather today. I fact the weather is not immaterial to user testing, especially user experience evaluation, as bad weather often effects people’s moods, and if people are less happy walking in to your study they are likely to perform less well and record lower satisfaction!
If you are performing a controlled experiment, you might try to do things strictly to protocol, but there may be slight differences in the way you do things that push the experiment in one direction or another.
Some years ago I was working on hydraulic sprays, as used in farming. We had a laser-based drop sizing machine and I ran a series of experiments varying things such as water temperature and surfactants added to the spray fluid, in order to ascertain whether these had any effect on the size of drops produced. The experiments were conducted in a sealed laboratory and were carefully controlled. When we analysed the results there were some odd effects that did not seem to make sense. After puzzling over this for some while one of my colleagues remembered that the experiments had occurred over two days and suggested we add a ‘day effect’ to the analysis. Sure enough this came out as a major factor and once it was included all the odd effects disappeared.
Now this was a physical system and I had tried to control the situation as well as possible, and yet still there was something, we never worked out what, that was different between the two days. Now think about a user test! You cannot predict every odd effect, but as far as you can make sure you mix your conditions as much as possible so that they are ‘balanced’ with respect to other factors can help – for example if you are doing two sessions of experimentation try to have a mix of two systems you are comparing in each session (although I know not always possible).
experimenter effects – A particular example of a contextual factor that may affect users performance and attitude is you! You may have prepared a script so that you greet each user the same and present the tasks they have to do in the same way, but if you have had a bad day your mood may well come through.
Using pre-recorded or textual instructions can help, but it would be rude to not at least say “hello” when they come in, and often you want to set users at ease so that more personal contact is needed. As with other kinds of context effect, anything that can help balance out these effects is helpful. It may take a lot of effort to set up different testing systems, so you may have to have a long run of one system testing and then a long run of another, but if this is the case you might consider one day testing system A in the morning and system B in the afternoon and then another day doing the opposite. If you do this, then, even if you have an off day, you affect both systems fairly. Similarly if you are a morning person, or get tired in the afternoons, this will again affect both fairly. You can never remove these effects, but you can be aware of them.
The second kind of independence is between the various causal factors that you are measuring things about. For example, if you sampled LinkedIn and WhatsApp users and found that 5% of LinkedIn users were Justin Beiber fans compared with 50% of WhatsApp users, you might believe that there was something about LinkedIn that put people off Justin Beiber. However, of course, age will be a strong predictor of Justin Beiber fandom and is also related to the choice of social network platform. In this case social media use and age are called confounding variables.
As you can see it is easy for these effects to confuse causality.
A similar, and real, example of this is that when you measure the death rate amongst patients in specialist hospitals it is often higher than in general hospitals. At first sight this makes it seem that patients do not get as good care in specialist hospitals leading to lower safety, but in fact this is due to the fact that patients admitted to specialist hospitals are usually more ill to start with.
This kind of effect can sometimes entirely reverse effects leading to Simpson’s Paradox.
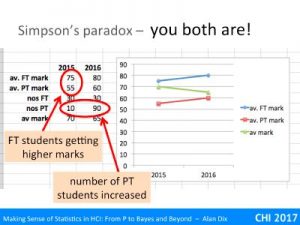
Imagine you are teaching a course on UX design. You teach a mix of full-time and part-time students and you have noticed that the performance of both groups has been improving year on year. You pat yourself on the back, happy that you are clearly finding better ways to teach as you grow more experienced.
However, one day you get an email from the university teaching committee noting that your performance seems to be diminishing. According to the university your grades are dropping.
Who is right?
In fact you may both be.
In your figures you have the average full-time student marks in 2015 and 2016 as 75% and 80%, an increase of 5%. In the same two years the average part-time student mark increased from 55% to 60%.
Yes both full-time and part-time students have improved their marks.
The university figures however show an average overall mark of 70% in 2015 dropping to 65% in 2016 – they are right too!
Looking more closely whilst there were 30 full-time students in both years the number of part-time students had increased form 10 in 2015 to 90 in 2016, maybe due to a university marketing drive or change in government funding patterns. Looking at the figures, the part-time students score substantially lower than the full-time students, not uncommon as part-time students are often juggling study with a job and may have been out of education for some years. The lower overall average the university reports entirely due to there being more low-scoring part-time students.
Although this seems like a contrived example see [BH75] for a real example of Simpson’s Paradox. Berkeley appeared to have gender bias in admission because (at the time, 1973) women had only 35% acceptance rate compared with 44% for men. However, deeper analysis found that in individual departments the bias was, if anything, slightly towards female candidates, it was just that females tended to apply for more competitive courses with lower admission rates (possibly revealing discrimination earlier in the education process).
Simpson's paradox explained in a gif pic.twitter.com/LETNm6Y9ea
— Rafael Irizarry (@rafalab) July 28, 2017
Finally the way you obtain your sample may create lack of independence between your subjects.
This itself happens in two ways:
internal non-independence – This is when subjects are likely to be similar to one another, but in no particular direction with regard to your question. A simple example of this would be if you did a survey of people waiting in the queue to enter a football match. The fact that they are next to each other in the queue might mean they all came off the same coach and so more likely to supporting the same team.
Snowball samples are common in some areas. This is when you have an initial set of contacts, often friends or colleagues, use them as your first set of subjects and then ask them to suggest any of their own contacts who might take part in your survey.
Imagine you do this to get political opinions in the US and choose your first person to contact randomly from the electoral register. Let’s say the first person is a Democrat. That person’s friends are likely to likely to share political beliefs and also be Democrat, and then their contacts also. Your Snowball sample is likely to give you the impression that nearly everyone is a Democrat!
Typically this form of internal non-independence increases variability, but does not create bias.
Imagine continuing to survey people in the football queue, eventually you will get to a group of people from a different coach. Eventually after interviewing 500 people you might have thought you had pretty reliable statistics, but in fact that corresponds to about 10 coaches, so will have variability closer to a sample size of ten. Alternatively if you sample 20, and colleagues also do samples of 20 each, some of you will think nearly everyone are supporters of one team, some will get data that suggest the same is true for the other team, but if you average your results you will get something that is unbiased.
A similar thing happens with the snowball sample, if you had instead started with a Republican you would likely to have had a large sample almost all of whom would have been Republican. If you repeat the process each sample may be overwhelmingly one party or the other, but the long term-average of doing lots of Snowball samples would be correct. In fact, just like doing a bigger sample on the football queue, if you keep on the Snowball process on the sample starting with the Democrat, you are likely to eventually find someone who is friends with a Republican and then hit a big pocket of Republicans. However, again just like the football queue, while you might have surveyed hundreds of people, you may have only sampled a handful of pockets, the lack of internal independence means the effective sample size is a lot smaller than you think.
external non-independence – This is when the choice of subjects is actually connected with the topic being studied. For example, asking visiting an Apple Store and doing a survey about preferences between MacOs and Windows, or iPhone and Android. However, the effect may not be so immediately obvious, for example, using a mobile app-based survey on a topic which is likely to be age related.
The problem with this kind of non-independence is that it may lead to unintentional bias in your results. Unlike the football or snowball sample examples, doing another 20 users in the Apple Store, and then another 20 and then another 20 is not going to average out the fact that it is an Apple Store.
The crucial question to ask yourself is whether the way you have organised your sample likely to be independent of the thing you want to measure.
In the snowball sample example, it is clearly problematic for sampling political opinions, but may me acceptable for favourite colour or shoe size. The argument for this may be based on previous data, on pilot experiments, or on professional knowledge or common sense reasoning. While there may be some cliques, such as members of a basketball team, with similar shoe size, I am making a judgement based on my own life experience that common shoe size is not closely related to friendship whereas shared political belief is.
The decision may not be so obvious, for example, if you run a Fitts’ Law experiment and all the distant targets are coloured red and the close ones blue. Maybe this doesn’t matter, or maybe there are odd peripheral vision reasons why it might skew the results. In this case, and assuming the colours are important, my first choice would be to include all conditions (including red close and blue distant targets) as well as the ones I’m interested in, or if not run and alternative experiment or spend a lot of time checking out the vision literature.
Perhaps the most significant potential biasing effect is that we will almost always get subjects from the same society as ourselves. In particular, for university research this tends to mean undergraduate students. However, even the most basic cognitive traits are not necessarily representative of the world at large [bibref name=”HH10″ /], let along more obviously culturally related attitudes.
References
[BH75] Bickel, P., Hammel, E., & O’Connell, J. (1975). Sex Bias in Graduate Admissions: Data from Berkeley. Science, 187(4175), 398-404. Retrieved from http://www.jstor.org/stable/1739581
[HH10] Henrich J, Heine S, Norenzayan A. (2010). The weirdest people in the world? Behav Brain Sci. 2010 Jun;33(2-3):61-83; discussion 83-135. doi: 10.1017/S0140525X0999152X. Epub 2010 Jun 15.