ambiguous(e){
p,q,r
P : I(p)=e=I(q) and I(pr)
I(qr)}
Alan Dix
& Colin
Runciman
at time of publication: Department of Computer Science, University of York,
UK
Paper presented at HCI'85, London..
Full reference:
A. J. Dix and C. Runciman (1985).
Abstract models of interactive systems.
People and Computers: Designing the Interface, Ed. P. J. &. S. Cook. Cambridge University Press. pp. 13-22.
http://www.hcibook.com/alan/papers/PIE85/
For related work see Alan's topics pages on formal methods in HCI and undo
Abstract: We propose an abstract model for a large class of interactive systems. In these systems the user provides a sequence of commands that determines both a corresponding sequence of displays and a net effect or result. Editors, for example, usually fit this model. We show how our model can be used to address issues such as display laws, error correction, exception handling and command types. We give some formal statements of design principles, and also discover ways in which these interact or even conflict. Such results are of value whether or not a formal development method is used.
It is often suggested that there are domain-independent design principles for the human interface of interactive systems. Thimbleby proposes that these principles be stated both colloquially, to help users develop a suitable model of the system, and formally, for use in system development (Thimbleby 1984). However, a formal statement can only be made in the context of some assumed structure of the relevant system. Hence it may be difficult to transfer formal principles from one system to another. It may even be that by the time formal specification has reached the stage where the design principles can be stated, important decisions have been made which violate them.
One possible solution is to develop an abstract model of the class of systems we want to study and to state the formal principles within this framework. When a specific system is designed, the abstract principles can be used to derive, or at least to constrain, the formal specification. Also theorems about the abstract model should aid understanding of the interactions between various principles and hence aid design.
Because we are interested in the human interface of a computer system we want our model to refer only to what can be perceived by the user. To the user the system is described by the possible inputs and the effects these have. We view input as a sequence of commands from an allowable set (call it C). We call any such sequence of commands a program, and call the set of all programs P. The set of possible effects we call E: depending on what properties of the system we are trying to formalize, an effect may correspond variously to a VDU screen image, some richer form of current state, or whatever else we choose.
The relation between the command sequence entered so far and its net effect is a function I (for interpretation) from P to E and we assume that every effect can be obtained by some program. So triples <P,I,E> are simple machines, which we will call PIEs.
The first set of properties capture what the current effect tells us about the future effect, that is the observability of the relevant internal states, or the predictability of the system. This could be thought of as the "gone for a cup of tea" problem. When you return and have forgotten precisely what you typed to get where you are, does the current effect contain enough information to enable you to decide what commands to issue in future?
It may be that two programs have the same current effect but when identically extended yield different effects. We then say that the original effect is ambiguous, as more than one internal state is possible.
If no effect is ambiguous then things that look the same are the same. We call a PIE that has this property monotone.ambiguous(e)
If we model a system by identifying effects with single VDU images, say, monotonicity is far too restrictive to be a sensible requirement: a system obeying it could be little more than a notice board on the screen. Exactly what constitutes a more reasonable idea of a viewable effect, for which monotonicity is an appropriate requirement, we consider later.monotonep,q,r
I(pr)=I(qr)}
Although any effect can be reached as the result of some sequence of commands, this leaves open the possibility of "blind alleys". Some command sequence might forever seal the user off from a particular effect. For instance, a hastily implemented editor might forbid further amendments in a section that has been cut and pasted. To legislate against such a system we may require the strong reachability property.
That is "not only can you get anywhere but you can get anywhere from anywhere". In an editor, strong reachability assures us that the user is able to change any part of the document at any stage. (It says nothing about the effort required to make changes; we would need a lot more structure to formalize "flexibility and ease of use".)strong reachability
In a non-monotone PIE, perhaps modelling displays as effects, a single effect may hide many underlying states and we may wish to be able to reach any of these states. This requirement we call mega reachability!
Both reachability conditions seem reasonable for editors in most circumstances. The only exceptions would be things like a startup banner - an effect that cannot sensibly recur.mega reachability
One problem with the PIE model is the lack of structure in the effect space to reflect the richness of even modest displays such as two dimensional arrays of characters on a VDU. This problem can be overcome by successive refinement of the model until appropriate properties and requirements can be stated. Note, however, that many useful properties can be formulated even without such refinement; and, as we have already observed, it is desirable to express requirements at the most abstract level possible.
An important refinement is to distinguish those parts of the effect that are part of the interactive process from those that are concerned with the finished product. To do this we assume that from our effect space E there are two maps, display and result, to spaces D and R respectively. These correspond to the immediately visible display and to the product that would be obtained if the current effect were taken as final.
We refer to this structure as a RED-PIE.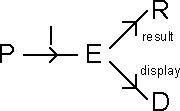
As we now have the distinction between the immediate display and the result, we can more usefully apply the reachability conditions described above. Although we do not necessarily expect the display to satisfy all our reachability conditions, it is reasonable to expect that whatever we have done so far it is still possible to produce any desired final output. That is, formally, for any RED-PIE, the PIE <P, result o I, R> should satisfy the strong reachability requirement.
It is less clear what parts of a system should be monotone. The display is an obvious choice, as this is what the user actually sees, but <P, display o I, D> cannot be monotone in general because the VDU doesn't contain enough information to describe even its own future state, let alone that of the whole system. On the other hand if we demand that <P, result o I, R> is monotone this is tantamount to forbidding concepts such as "current item" which are fundamental to many programs.
As a user, "what you see" at any moment is a display image. To observe the present result and to predict the effect of subsequent commands, this single image is rarely adequate. But there may be ways of viewing more than this without changing the result. These might rely on simple algorithms such as "go to the top of the file, scroll through it to the end, go back to where you started". Such an algorithm we call a .strategy and the resulting wider views the observable effects (O). This new space fits into the RED-PIE picture as follows.
Using this wider notion of "what you see" we can state some display laws. First, to be able to work out from O what the result will be, we expect a map from O to R, giving the current result. If we also required that the observable effect inform us about the internal state of the process we could request a map O->E.
We could make our requirements even stronger. Having used the strategy to work out what the result would be we could demand that the result together with the display should contain sufficient information for all use of the editor, and ask for a map DxR->E. The user of an editor satisfying this requirement, armed with an up-to-date listing and only looking at the current display, knows everything. This sounds like a useful property, but it does put quite severe restrictions on other aspects of the editor design.
There must be restrictions on the sort of strategies that are considered reasonable. For instance "delete line down until you've seen to the end of the file then delete up till you've seen to the top" may indeed display all the file but is obviously silly. Instead, strategies should always produce passive programs. Passive programs are those that change the view of the result but not the result itself. Using the notation result(x) as a shorthand for result(I(x)), we can give the following definition of passive programs.
So results before and after a passive program are the same, though displays and internal states may differ. Still further, one might require only strategies that begin and end in the same state.passive(p)
The ability to spot errors quickly is one of the advantages of highly interactive computing. But this ability is only appealing if the correction is just as easy! A weak form of error correction has already been described in the reachability conditions: if we can get anywhere from anywhere, then in particular, if we do something wrong we can get back to the position before the mistake. But the definitions of the reachability conditions involve the entire program. It is more attractive if error recovery is incremental, depending only on mistakenly entered commands, because typically these are most recent and are short.
Imagine a user telephoning an advisor with the request "I've just done so-and-so and now I seem to be stuck; how can I get out of it?". We are hypothesising a design requirement that a helpful reply always exists, without the need for further information.
{ function undo (P->P) :
{ p,q P : I(p q undo(q))=I(p)}}
Demanding such an undo for all sequences p can have unwelcome side
effects.
One possible consequence is that not only would there exist an undo for
each command, but that they would all have to be different!
Thus knowing only that there
exists
a way of undoing any action is of little comfort, we must also ask how
easy it is to remember and to perform.
A more realistic requirement is an editor with both ordinary commands, and a small distinguished set of undo commands. Ordinary commands obey much more stringent rules than undo commands under the assumption that the latter are used more cogently. The class of ordinary commands may include some commands that have undos (e.g. letters undone with delete), some commands that behave like sub-groups containing mutual inverses (e.g. cursor movement), and others like delete itself with no undo. The special undo commands would then be added. Note that even if some commands like cursor right/left have inverses relative to the ordinary commands these may be lost when new undo commands are added.
Formally we have two alphabets C and U. We then have P, the sequences from C, and Pu, the set of sequences from C+U. The following laws reflect possible requirements.
{ function undo (P->Pu) :
{ p,q,r P : I(p q undo(q) r)=I(pr)}}
{ function undo (C->C+U) :
{ p,r P, c C : I(p c undo(c) r)=I(pr)}}
Undo mechanisms can get quite sophisticated, ranging from the simple restoration of delete buffers to the keeping of entire session history trees (Vitter 1984). The selection of a particular mechanism may have consequences that are not immediately apparent. For example, consider editors that retain a command and editor state history. If we want to preserve monotonicity this history must be part of the observable effect. That is, there must be commands for perusing this structure (they might be included in the undo procedure itself). If reachability issues are to be taken seriously the designers task becomes still more complex.
System designers often begin with an idealised system, such as an editor with an unbounded text length or a graphics device with arbitrary resolution. Turning this ideal into a running system introduces various boundary conditions. The user of a system may also have an idealised model: for instance, "up-line followed by down-line gets me back where I started" (c.f. undo above). This model too fails at boundaries. For a system designed with user engineering in the foreground the two ideal views should correspond.
Given that some properties of the ideal system fail in the actual system we might expect that when an exception arises there is some consistent system action. That the system warns the user by some means - bell, flashing light, or whatever - goes without saying.
Suppose we have two PIEs <P,I,E>, the ideal and <P,I',E'>, the
exception PIE,
related by a map proj from E' to E.
There is a boolean function ex on the elements of P,
that satisfies ex(p) ex(pq) for all q, and
the following diagram commutes on the set ok(P) = {p:P | not ex(p)}.
That is I(p) = proj(I'(p)) unless ex(p).
One likely GUEP for exceptions is "no guesses": when a command causes an exception to be raised, subsequent commands behave as if the command had never been issued.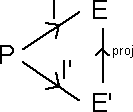
Or there is a weaker condition."no guesses"
This just says that when an exception is raised at least the position you are left in is one that could have been reached by legitimate means."nothing silly"
A tentative basis on which to choose between the alternative requirements is that "nothing silly" is appropriate where the exception is associated with a limit of the system, but "no guesses" should apply where the user has made an error. For example, line break algorithms for most editors follow "nothing silly", but cuts without previous marks follow "no guesses" - not deleting the entire document up to the cut point, say! We can also reformulate our request for undos, only asking for an undo when an exception has not occurred.
We have already introduced the class of passive programs. There are other classes that could play important roles in formal requirements. To take just one other example consider the distinction between global and local commands.
One characterization of global commands is that they can be modelled by a function R->R. That is, the meaning of a global command does not depend on any extra information such as position, mode or context. To determine what the result is after the command one need only know what the result was before it.
For local commands we might demand the ability to spot and correct mistakes easily. We can express such a requirement as follows (L being the local commands).
So if we intend something (c), but accidently type something else (c'), and the mistake matters, then we can see it in the display."mistakes in local commands are obvious"
Put informally, the displays before and after each command are enough to determine a command sequence by which the command could be undone."local commands suggest their inverses"
We have shown that a very simple model can be used to address a variety of design requirements in interactive systems. We have used editors to illustrate this. Requirements can be captured as constraints on the model and hence on system design. Because they are formal requirements, they are open to proof for any given implementation (Walker et. al. 1980). They are also open to analysis that can uncover subtle interactions between different design choices.
There are weaknesses in the PIE approach. Questions of a temporal nature are difficult to frame. Most of our current formalizations take the form of existence laws and we have yet to see how useful laws of this kind are to users: does the knowledge that it is possible to see the entire document using only safe commands, and that any mistakes can be undone, help users by giving confidence, or do they require actual constructive ways of doing these things to be embodied in simple rules?
We should also like to find refinements specifying more closely the kinds of structure that must exist for claims like "what you see is what you get" to be valid.
As a research team we have found that one of the biggest gains is simply having a common currency for discussing (often quite loosely) the various properties that interest us. In a companion paper (Harrison & Thimbleby 1985) our colleagues examine the potential usefulness of the approach in a wider context.