Linear discriminant analysis attempts to create one or more linear functions to separate known classes. In the case of two classes and 2D data this is simply a line that runs between the classes. Ideally the classes are completely separated by the linear functions, but in some case this may be impossible, either because of noise blurring the boundaries (in which case the linear discrimant may still be a good classifier), or because the classes are not linearly separable.
Used in Chap. 6: page 85; Chap. 7: page 92
Also known as: linear discriminant
Used in glossary entries: linearly separable
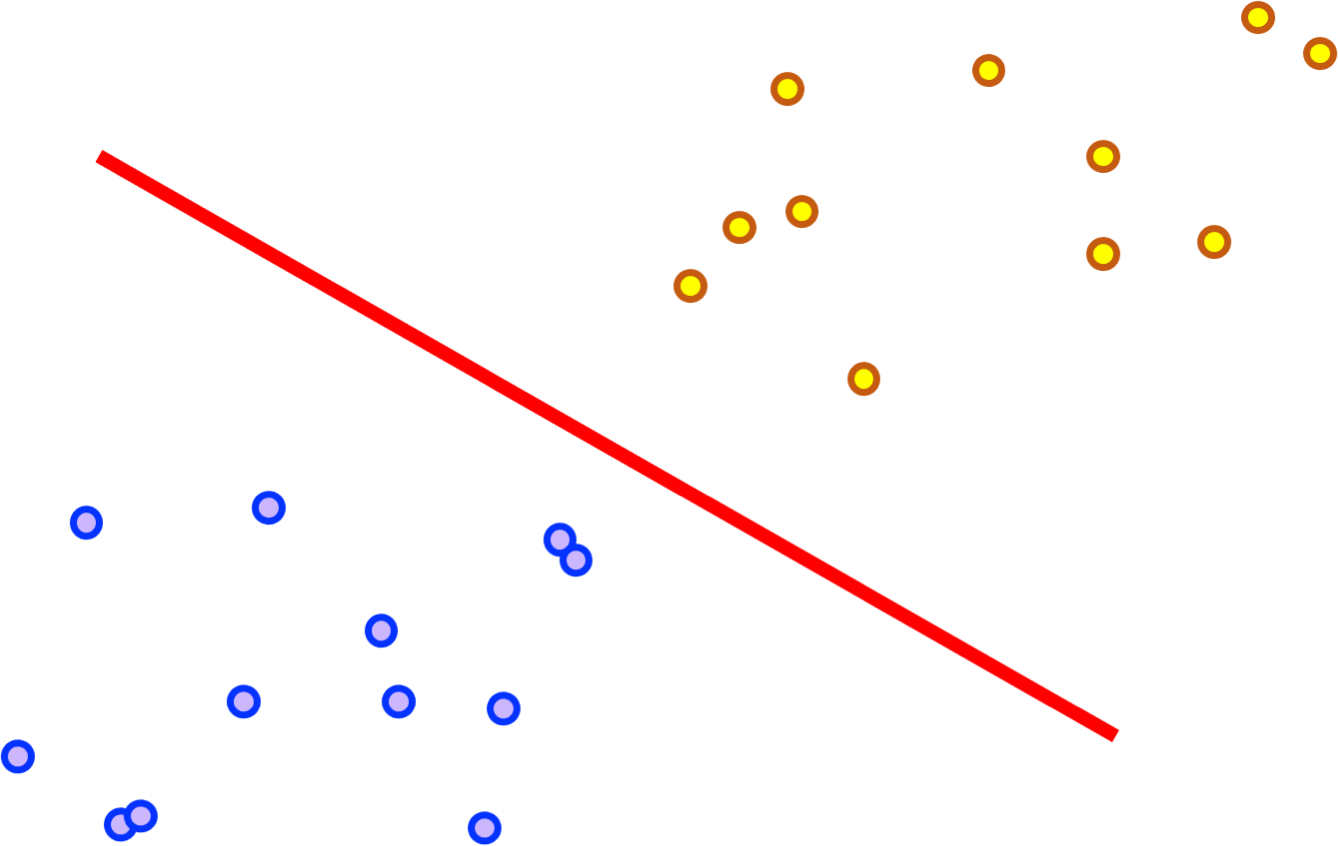
Linearly separable clusters