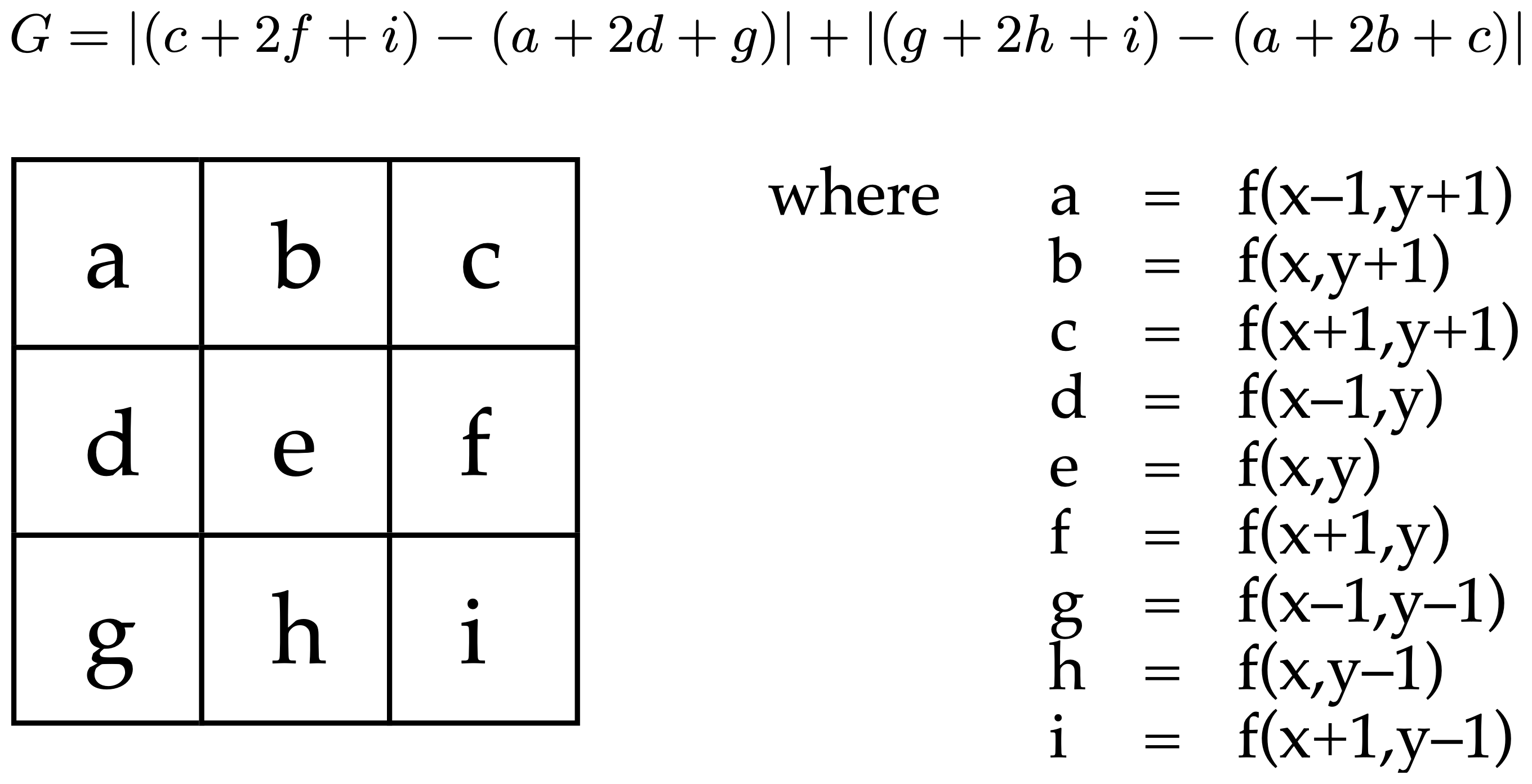
Sobel's operator is used to assess whether there is a line at a particular location and to estimate its direction. It can be seen as the sum of two factors, one measuring the horizontal rate of change and the other the vertical rate of change.
H = (c+2f+i) - (a+2d+g)
V = (g+2h+i) - (a+2b+c)
G = | H | + | V |
where ,a,b,c,d,e,f,g,h,i are the pixels in a 3x3 square (see diagram)
H = (c+2f+i) - (a+2d+g)
V = (g+2h+i) - (a+2b+c)
G = | H | + | V |
where ,a,b,c,d,e,f,g,h,i are the pixels in a 3x3 square (see diagram)
Used in Chap. 12: pages 168, 169, 181, 187
Sobel's operator