One set of strategies for gaining power are about the way you choose and manage your participants.

We will see strategies that address all three aspects of the noise–effect–number triangle:

• more subjects or trials (increase number)
• within subject/group (reduce noise)
• matched users (reduce noise)
• targeted user group (increase effect)

First of all is the most common approach: to increase either the number of subjects in your experiment or study, or the number of trials or measurements you make for each one.

Increasing the number of subjects helps average out any differences between subjects due to skill, knowledge, age, or simply the fact that all of us are individuals.

Increasing the number of trials (in a controlled experiment), or measurements, can help average out within subject variation. For example, in Fitts’ Law experiments, given the same target positions, distances and sizes, each time you would get a different response time, it is the average for an individual that is expected to obey Fitts’ Law.

Of course, whether increasing the number of trials or the number of subjects, the points, that we’ve discussed a few times already, remains — you have t increase the number a lot to make a small difference in power. Remember the square root in the formula. Typically to reduce the variation of the average by two you need to quadruple the number of subjects or trials; this sounds do-able. However, if you need to decrease the variability of the mean by a factor of then then you need one hundred times as many participants or trials.

In Paul Fitts’ original experiment back in 1954 [Fi54], he had each subject try 16 different conditions of target size and distance, as well as two different stylus weights. That is he was performing what is called a within subjects experiment.

An alternative experiment could have taken 32 times as many participants, but have each one perform for a single condition. With enough participants this probably would have worked, but the number would probably have needed to be enormous.

For low-level physiological behaviour, the expectation is that even if speed and accuracy differ between people, the overall pattern will be the same; that is we effectively assume between subject variation of parameters such as Fitts’ Law slope will be far less than within subject per-trial variation.

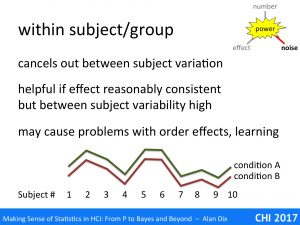
Imagine we are comparing two different experimental systems A and B, and have recorded users’ average satisfaction with each. The graph in the slide above has the results (idealised not real data). If you look at the difference for each system A is always above system B, there is clearly an effect. However, imagine jumbling them up, as if you had simply asked two completely different sets of subjects, one for system A and one for system B – the difference would probably not have shown up due to the large between subject differences.

The within subject design effectively cancels out these individual differences.

Individual differences are large enough between people, but are often even worse when performing studies involving groups of people collaborating. As well as the different people within the groups, there will be different social dynamics at work within each group. So, if possible within group studies perhaps even more important in this case.

However, as we have noted, increased power comes with cost, in the case of within subject designs the main problem is order effects.

For a within subjects/groups experiment, each person must take part in at least two conditions. Imagine this is a comparison between two interface layouts A and B, and you give each participant system A first and then system B. Suppose they perform better on system B, this could simply be that they got used to the underlying system functionality — a learning effect. Similarly, if system B was worse, this may simply be that users got used to the particular way that system A operated and so were confused by system B — an interference effect.

The normal way to address order effects, albeit partially, is to randomise or balance the orders; for example, you would do half the subjects in the order A–B and half in the order B–A. More complex designs might include replications of each condition such as ABBA, BAAB, ABAB, BABA.

Fitts’ original experiment did a more complex variation of this, with each participant being given the 16 conditions (of distance and size) in a random order and then repeating the task later on the same day in the opposite order.

These kinds of designs allow one to both cancel out simple learning/interference effects and even model how large they are. However, this only works if the order effects are symmetric; if system A interferes with system B more than vice versa, there will still be underlying effects. Furthermore, it is not so unusual that one of the alternatives is the existing one that users are used to in day-to-day systems.

There are more sophisticated methods, for example giving each subject a lot of exposure to each system and only using the later uses to try to avoid early learning periods. For example, ten trials with system A followed by ten with system B, or vice versa, but ignoring the first five trials for each.

For within-subjects designs it would be ideal if we could clone users so that there are no learning effects, but we can still compare the same user between conditions.

One way to achieve this (again partially!) is to have different user, but pair up users who are very similar, say in terms of gender, age, or skills.

This is common in educational experiments, where pre-scores or previous exam results are used to rank students, and then alternate students are assigned to each condition (perhaps two ways to teach the same material). This is effectively matching on current performance.

Of course, if you are interested in teaching mathematics, then prior mathematics skills are an obvious thing to match. However, in other areas it may be less clear, and if you try to match on too many attributes you get combinatorial explosion: so many different combinations of attributes you can’t find people that match on them all.

In a way matching subjects on an attribute is like measuring the attribute and fittings a model to it, except when you try to fit an attribute you usually need some model of how it will behave: for example, if you are looking at a teaching technique, you might assume that post-test scores may be linearly related to the students’ previous year exam results. However, if the relationship is not really linear, then you might end up thinking you have fond a result, which was in fact due to your poor model. Matching subjects makes your results far more robust requiring fewer assumptions.

A variation on matched users is to simply choose a very narrow user group. In some ways you are matching by making them all the same. For example, you may deliberately choose 20 year old college educated students … in fact you may do that by accident if you perform your experiments on psychology students! Looking back at Fitts original paper [Fi54] says, “Sixteen right-handed college men serves as Ss (Subjects)”, so there is good precident. By choosing participants of the same age and experience you get rid of a lot of the factors that might lead to individual differences. Of course there will still be personal differences due to the attributes you haven’t constrained, but still you will be reducing the overall noise level.

The downside of course, is that this then makes it hard to generalise. Fitts’ results were for right-handed college men; do his results also hold for college women, for left-handed people, for older or younger or less well educated men? Often it is assumed that these kinds of low level physiological experiments are similar in form across different groups of people, but this may not always be the case.

Henrich, Heine and Norenzayan [HH10] reviewed at a number of psychological results that looked as though they should be culturally independent. The vast majority of fundamental experiments were performed on what they called WEIRD people (Western, Educated, Industrialized, Rich, and Democratic), but where there were results form people of radically different cultural backgrounds, there were often substantial differences. This even extended to low-level perceptions.

You may have seen the Müller-Lyer illusion: the lower line looks longer, but in fact both lines are exactly the same length. It appears that this illusion is not innate, but due to being brought up in an environment where there are lots of walls and rectilinear buildings. When children and adults from tribes in jungle environments are tested, they do not perceive the illusions and see the lines as the same length.

We can go one step further and deliberately choose a group for whom we believe we will see the maximum effect. For example, imagine that you have designed a new menu system, which you believe has a lower short-term memory requirement. If you test it on university students who are typically young and have been honing their memory skills for years, you may not see any difference. However, short-term memory loss is common as people age, so if you chose more elderly users you would be more likely to see the improvements due to your system.

In different circumstances, you may deliberately choose to use novice users as experts may be so practiced on the existing system that nothing you do makes any improvement.

The choice of a critical group means that even small differences in your system’s performance have a big difference for the targeted group; that is you are increasing the effect size.

Just as with the choice of a narrow type of user, this may make generalisation difficult, only more so. With the narrow, but arbitrary group, you may argue that in fact the kind of user does not matter. However, the targeted choice of users is specifically because you think the criteria on which you are choosing them does matter and will lead to a more extreme effect.

Typically in such cases you will use a theoretical argument in order to generalise. For example, suppose your experiment on elderly users showed a statistically significant improvement with your new system design. You might then use a combination of qualitative interviews and detailed analysis of logs to argue that the effect was indeed due to the reduced short-term memory demand of your new system. You might then argue that this effect is likely to be there for any group of users, creating and additional load and that even though this is not usually enough to be apparent, it will be interfering with other tasks the user is attempting to do with the system.

Alternatively, you may not worry about generalisation, if the effect you have found is important for a particular group of users, then it will be helpful for them – you have found your market!

References

[Fi54] Fitts, Paul M. (1954) The information capacity of the human motor system in controlling the amplitude of movement. Journal of Experimental Psychology, 47(6): 381-391, Jun 1954,. http://dx.doi.org/10.1037/h0055392

[HH10] Henrich J, Heine S, Norenzayan A. (2010). The weirdest people in the world? Behav Brain Sci. 2010 Jun;33(2-3):61-83; discussion 83-135. doi: 10.1017/S0140525X0999152X. Epub 2010 Jun 15.