experiment with bias and independence
experiment with bias and independence
This section will talk you through two small web demonstrators that allow you to experiment with virtual coins.
Because the coins are digital you can alter their properties, make them not be 50:50 or make successive coin tosses not be independent of one another. Add positive correlation and see the long lines of heads or tails, or put in negative correlation and see the heads and tails swop nearly every toss.
Links to the demonstrators can be found at statistics for HCI resources.
Incidentally, the demos were originally created in 1998; my very first interactive web pages. It is amazing how much you could do even with 1998 web technology!
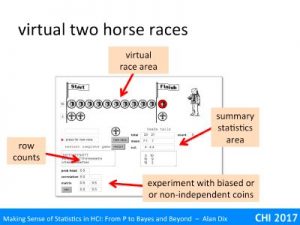
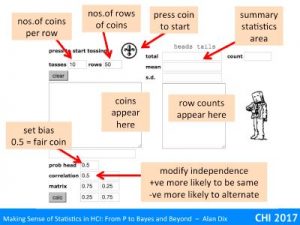
The first application automates the two-horse races that you have done by hand with real coins in the “unexpected wildness of random” exercises. This happens in the ‘virtual race area’ marked in the slide.
So far this doesn’t give you any advantage over physical coin tossing unless you find tossing coins very hard. However, because the coins are virtual, the application is able to automatically keep a tally of all the coin tosses (in the “row counts” area), and then gather statistics about them (in the “summary statistics area”).
Perhaps most interesting is the area marked “experiment with biased or non-independent coins” as this allows you to create virtual coins that would be very hard to replicate physically.
We’ll start with the virtual race area.
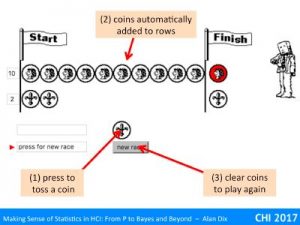
It should initially be empty. Press the marked coin to toss a coin. It will spin and when it stops the coin will be added to the top row for heads or the lower row for tails. Press the coin again for the next toss until one side or other wins.
If you would like another go, just press the ‘new race’ button.
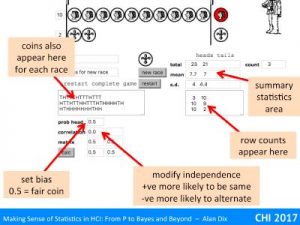
As you do each race you will see the coins also appear as ‘H’ and ‘T’ in the text area on the left below the coin toss button and the counts for each completed race appear in the text box to the right of that.
The area above that box on the right keeps a tally of the total number of heads and tails, the mean (arithmetic average) if heads and tails per race, and the standard of each. We’ll look at these in more detail in ‘more coin tossing’ below.
Finally the area at the bottom left allows you to create unreal coins!
Adjusting the “prob head” allows you to create biased coins (valid values between 0 and 1). For example, setting ‘prob head” to 0.2 makes a coin that will fall heads 20% of the time and tails 80% of the time (both on average of course!).
Adjusting the ‘correlation’ figure allows you to create coins that depend on the previous coin toss (valid values -1 to +1). A positive figure means that each coin is more likely to be the same as the previous one – that is if the previous coin was a head toy are more likely to also get a head on the next toss. This is a bit like a learning effect in . Putting a negative value does the opposite, if the previous toss was a head the next one is more likely to be tail.
Play with these values to get a feel for how it affects the coin tossing. However, do remember to do plenty of coin tosses for each setting otherwise all you will see is the randomness! Play first with quite extreme values, as this will be more evident.
The second application is very similar, except no race track!
This does not do a two-horse race, but instead will toss a given number of coins, and then repeat this. You don’t have to press the toss button for each cpin toss, just once and it does as many as you ask.
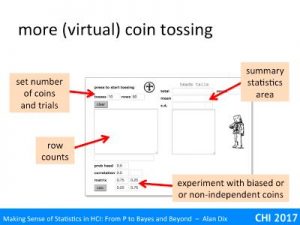
Instead of the virtual race area, there is just an area to put the number or coins you want it to toss, and then the number of rows of coins you want it to produce.
Let’s look in more detail.
At the top right are text areas to enter the number of coins to toss (here 10 coins at a time) and the number of rows of coins (here ste to 50 times). You press the coin to start, just as in the two-horse race, except now it will toss the coin 10 times and the Hs and Ts will appear in the tally box below. Once it has tossed the first 10 it will toss 10 more, and then 10 more until it has 50 rows of coins – 500 in total … all just for one press.
The area for setting bias and correlation is the same as in the two-horse race, as is the statistics area.
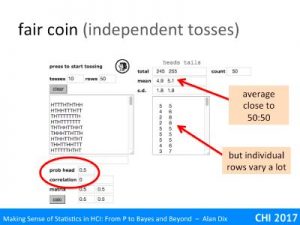
Here is a set of tosses where the coin was set to be fair (prob head=0.5) with completely independent tosses (correlation=0) – that is just like a real coin (only faster).
You can see the first 9 rows and first 9 row counts in the left and right text areas. Note how the individual rows vary quite a lot, as we have seen in the physical coin tossing experiments. However, the average (over 50 sets of 10 coin tosses) is quite close to 50:50. Note also the standard deviation
The standard deviation is 1.8, but note this is the standard deviation of the sample. Because this is a completely random coin toss, with well understood probabilistic properties, it is possible to calculate the ‘real’ standard deviation – this is the value you would expect to see if you repeated this thousands and thousands of times. This value is the square root of 2.5, which is just under 1.6. This measured standard deviation is an estimate of the ‘real’ value, and hence not the ‘real’ value, just like the measured proportion of heads has tuned out at 0.49, not exactly a half. This estimate of the standard deviation itself varies a lot … indeed estimates of variation of often very variable themselves!
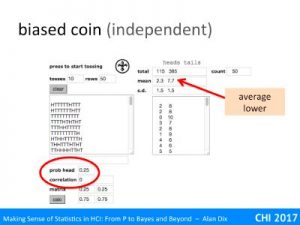
Here’s another set of tosses, this time with the probability of a head set to 0,25. That is a (virtual!) coin that falls heads about a quarter of the time. So a bit like having a four sided spinner with heads on one side and tails on the other three.
The correlation has been set to zero still so that the tosses are independent.
You can see how the proportion of heads is now smaller, on average 2.3 heads to 7.7 tails in each run of 10 coins. This is not exactly 2.5, but if you repeated this sometimes it would be less, sometimes more. On average, over 1000s of tosses it would end up close to 2.5.
Now we’re going to play with very unreal non-independent coins.
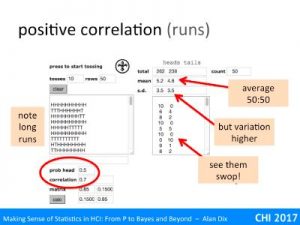
The probability of being a head is set to 0.5 so it is a fair coin, but the correlation is positive (0.7) meaning heads are more likely to follow heads and vice versa.
If you look at the left hand text area you can see the long runs of heads and tails. Sometimes they do alternate, but then sty the same for long periods.
Looking up to the summary statistics area the average numbers of heads and tails is near 50:50 – the coin was fair, but the standard deviation is a lot higher than in the independent case. This is very evident if you look at the right-hand text area with the totals as they swing between extreme values much more than the independent coin did (even more that its quite wild randomness!).
If we put a negative value for the correlation we see the opposite effect.
Now the rows of Hs and Ts alternate a lot of time, far more than a normal coin.
The average is still close tot 50:50, but this time the variation is lower and you can see this in the row totals, which are typically much closer to five heads and five tails than the ordinary coin.
Recall the gambler’s fallacy that if a coin has fallen heads lots of times it is more likely to be a tail next. In some way this coin is a bit like that, effectively evening out the odds, hence the lower variation.