In the first part of this two-part post, we saw that cycling into the wind takes far more additional effort than a tail wind saves.
 However, Will Wright‘s original question, “why does it feel as if the wind is always against you?” was not just about head winds, but the feeling that when cycling around Tiree, while the angle of the wind is likely to be in all sorts of directions, it feels as though it is against you more than with you.
However, Will Wright‘s original question, “why does it feel as if the wind is always against you?” was not just about head winds, but the feeling that when cycling around Tiree, while the angle of the wind is likely to be in all sorts of directions, it feels as though it is against you more than with you.
Is he right?
So in this post I’ll look at side winds, and in particular start with wind dead to the side, at 90 degrees to the road.
Clearly, a strong side wind will need some compensation, perhaps leaning slightly into the wind to balance, and on Tiree with gusty winds this may well cause the odd wobble. However, I’ll take best case scenario and assume completely constant wind with no gusts.
There is a joke about the engineer, who, when asked a question about giraffes, begins, “let’s first assume a spherical giraffe”. I’m not gong to make Will + bike spherical, but will assume that the air drag is similar in all directions.
Now my guess is that given the way Will is bent low over his handle-bars, he may well actually have a larger side-area to the wind than from in front. Also I have no idea about the complex ways the moving spokes behave as the wind blows through them, although I am aware that a well-designed turbine absorbs a fair proportion of the wind, so would not be surprised if the wheels added a lot of side-drag too.
If the drag for a side wind is indeed bigger than to the front, then the following calculations will be worse; so effectively working with a perfectly cylindrical Will is going to be a best case!
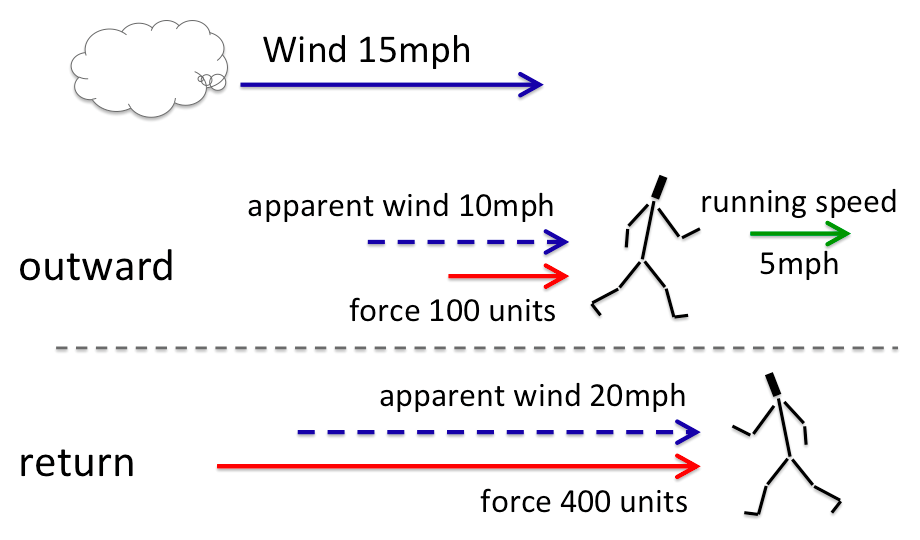
To make calculations easy I’ll have the cyclist going at 20 miles an hour, with a 20 mph side wind also.
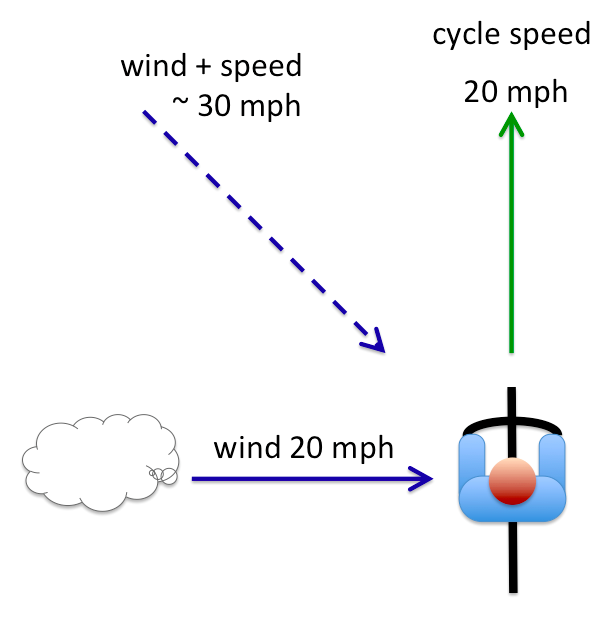
When you have two speeds at right angles, you can essentially ‘add them up’ as if they were sides of a triangle. The resultant wind feels as if it is at 45 degrees, and approximately 30 mph (to be exact it is 20 x √2, so just over 28mph).
Recalling the squaring rule, the force is proportional to 30 squared, that is 900 units of force acting at 45 degrees.
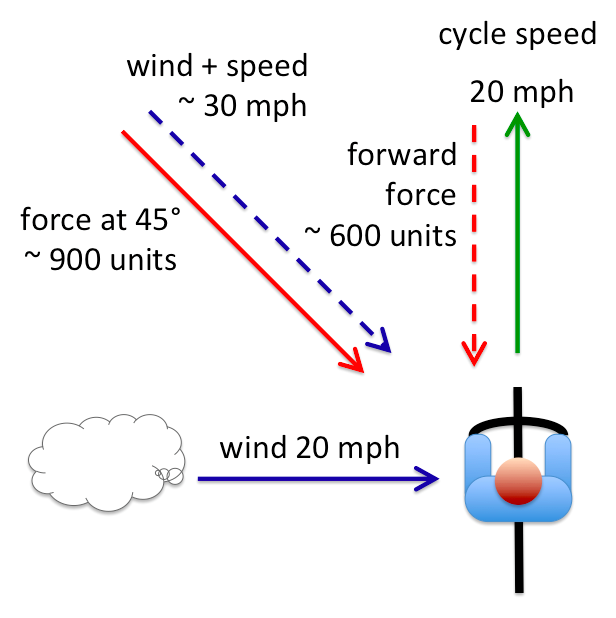
In the same way as we add up the wind and bike speeds to get the apparent wind at 45 degrees, we can break this 900 unit force at 45 degree into a side force and a forward drag. Using the sides of the triangle rule, we get a side force and forward drag of around 600 units each.
For the side force I’ll just assume you lean into (and hope that you don’t fall off if the wind gusts!); so let’s just focus on the forward force against you.
If there were no side wind the force from the air drag would be due to the 20 mph bike speed alone, so would be (squaring rule again) 400 units. The side wind has increased the force against you by 50%. Remembering that more than three quarters of the energy you put into cycling is overcoming air drag, that is around 30% additional effort overall.
Turned into head speed, this is equivalent to the additional drag of cycling into a direct head wind of about 4 mph (I made a few approximations, the exact figure is 3.78 mph).
This feels utterly counterintuitive, that a pure side wind causes additional forward drag! It perhaps feels even more counterintuitive if I tell you that in fact the wind needs to be about 10 degrees behind you, before it actually helps.
There are two ways to understand this.
The first is plain physics/maths.
For very small objects (around a 100th of a millimetre) the air drag is directly proportional to the speed (linear). At this scale, when you redivide the force into its components ahead and to the side, they are exactly the same as if you look at the force for the side-wind and cycle speed independently. So if you are a cyclist the size of an amoeba, side winds don’t feel like head winds … but then that is probably the least of your worries.
For ordinary sized objects, the squaring rule (quadratic drag) means that after you have combined the forces, squared them and then separated them out again, you get more than you started with!
The second way to look at it, which is not the full story, but not so far from what happens, is to consider the air just in front of you as you cycle.
You’ll know that cyclists often try to ride in each other’s slipstream to reduce drag, sometimes called ‘drafting’.

The lead cyclist is effectively dragging the air behind, and this helps the next cyclist, and that cyclist helps the one after. In a race formation, this reduces the energy needed by the following riders by around a third.
In addition you also create a small area in front where the air is moving faster, almost like a little bubble of speed. This is one of the reasons why even the lead cyclist gains from the followers, albeit much less (one site estimates 5%). Now imagine adding the side wind; that lovely bubble of air is forever being blown away meaning you constantly have to speed up a new bubble of air in front.
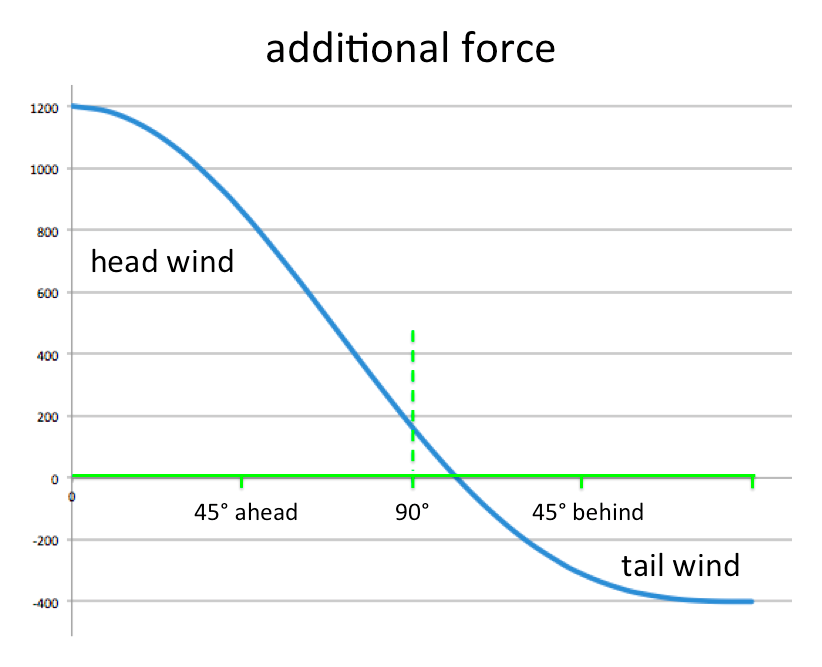
I did the above calculations for an exact side wind at 90 degrees to make the sums easier. However, you can work out precisely how much additional force the wind causes for any wind direction, and hence how much additional power you need when cycling.
Here is a graph showing that additional power needed, ranging for a pure head wind on the right, to a pure tail wind on the left (all for 20 mph wind). For the latter the additional force is negative – the wind is helping you. However, you can see that the breakeven point is abut 10 degrees behind a pure side wind (the green dashed line). Also evident (depressingly) is that the area to the left – where the wind is making things worse, is a lot more than the area to the right, where it is helping.
… and if you aren’t depressed enough already, most of my assumptions were ‘best case’. The bike almost certainly has more side drag than head drag; you will need to cycle slightly into a wind to avoid being blown across the road; and, as noted in the previous post, you will cycle more slowly into a head wind so spend more time with it.
So in answer to the question …
“why does it feel as if the wind is always against you?”
… because most of the time it is!